Improving Parallel Cholesky Factorization

Created : November 01, 2021

Last week I was working on implementing parallel cholesky factorization on accelerators, using SYCL DPC++, though obtained performance was not impressive due to some points I recognized and noted here. Today I plan to expand on those points, while splitting factorization into computationally ordered and dependent steps, which eventually proves to attain better speed up than previous implementation of mine.

I abstractly start working with one symmetric positive definite square matrix A_{N x N}, which I convert into U_{N x N}. Obtaining the other half is as easy as performing a transpose of U_{N x N}, giving me L_{N x N}. Once both of these halves are computed, 👇 can be checked, while keeping it in mind that as these computations are performed on accelerated environments, some floating point errors are inevitable.

I begin with an easy step, where I first initialise U_{N x N} with A_{N x N} and then parallelly zero out lower triangular portion ( read cells below pivots ) of U_{N x N}. During the further course of computation I'll never need to access those memory locations. As lower triangular portion of matrix is not rectangular shaped, I have to spawn N x N parallel work-items to zero out cells below pivots, though a substantial number of work-items will do nothing useful, which I ensure using conditional statement --- sadly resulting into divergent control flow.

I write the respective kernel as 👇

Next I've to run through a set of steps for N-many rounds, as matrix dimension is N x N. During each round, I go through following 2 steps of computations, in-order, as they have computational dependency.

1. Pivot Calculation
2. Pivot Row Calculation

Actually during each of these N-rounds, a pivot is selected and all operations are performed around it. These operations only compute/ access cells above (or including) pivots i.e. upper triangular portion of matrix.

In first step of round-k, say pivot U_{k, k} is selected, all I do is atomically compute updated pivot value by subtracting squared values at cells U_{i, k} where 0 <= i < k. Primarily I spawned N x N work-items for this step and was using conditional statements so that only work-items representing cells above selected pivot are able to atomically update pivot, by subtracting squared value of self. But this results into divergent control flow, costing high, as most of work-items do nothing useful after work-groups are fetched for computation. But one thing I noticed, during this step only cells above/ including selected pivot are accessed, which opens up opportunity for only spawning k work-items, parallelly (and atomically) computing updated value of selected pivot U_{k, k}. 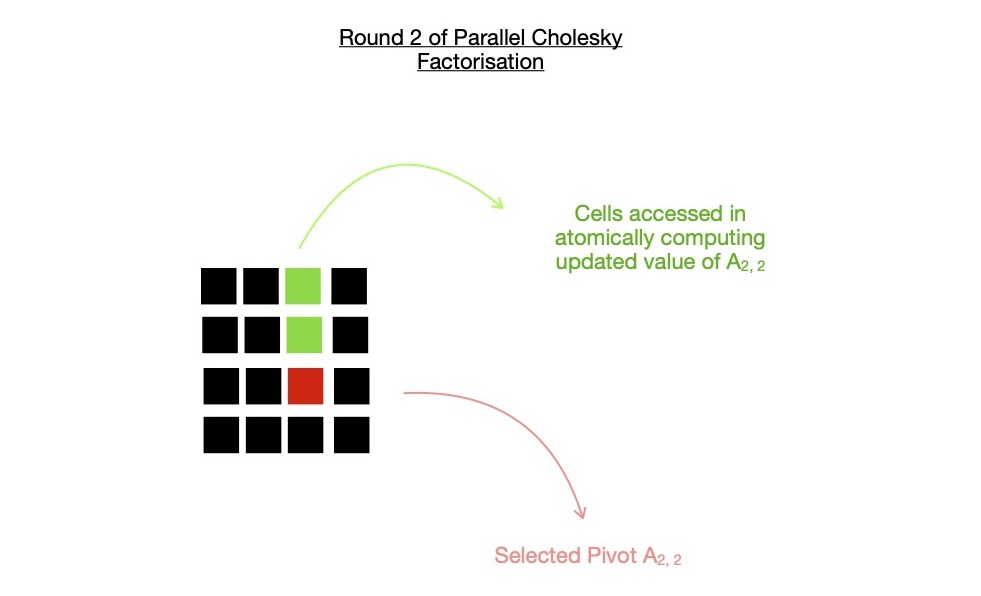In following diagram, I depict this step of round-k (= 2), by only spawning k(= 2) work-items, atomically computing selected pivot U_{2, 2}, by subtracting U_{i, 2}², where i = {0, 1}.

Before step one is completed, I've to spawn another kernel, for computing a single cell of U_{N x N}, by performing square root of selected pivot U_{k, k}. It's easy and cheap to spawn a kernel, which accesses single pivot cell and computes updated value, rather than implicitly transferring matrix data to host; computing same and finally again implicitly transferring data back to device. Data movement is expensive, costs lots of computation cycles and I aim to minimize so, which is why for improving performance I decide to spawn a single task kernel, which just updates selected pivot on device, while fully avoiding data movement --- low cost !

In second step, I compute updated values of cells, living on selected pivot row ( i.e. A_{k, _} ), to be more specific only those rightwards from pivot cell A_{k, k}. During this step, I need to access cells from a submatrix of dimension (k + 1) x (N - k). Following same logic as mentioned before, I decide to only spawn N - (k + 1) work-items, which removes need for using conditional statements, required when spawning N x N work-items, resulting into most work-items sitting idle. Notice, for any selected k ( >= 0 && < N ), only N - (k + 1) columns have column index higher than selected pivot on same row --- so this time no divergence in control flow, all work-items do something useful.

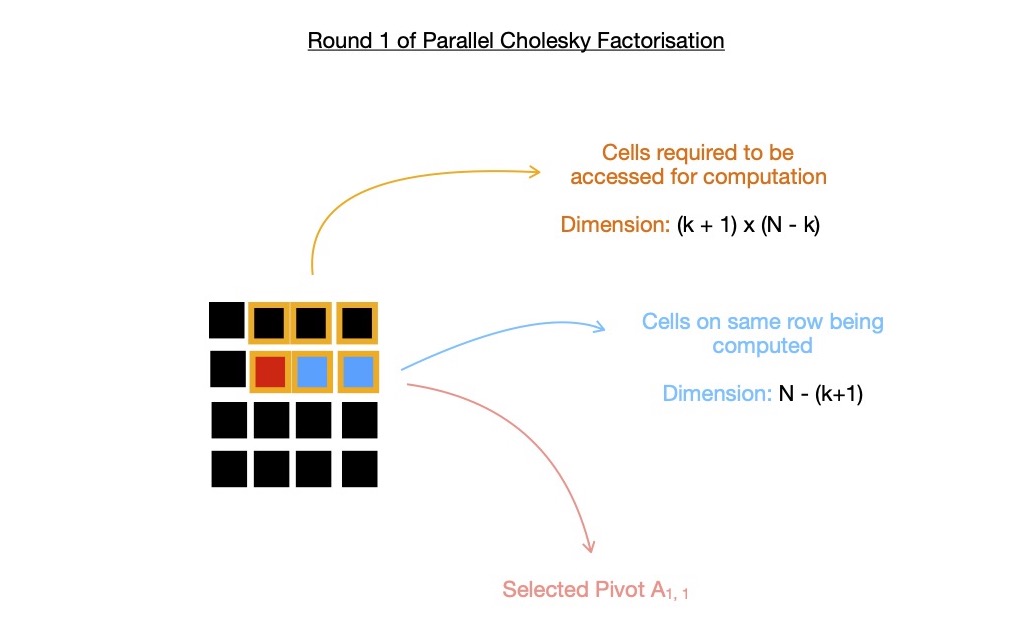
In following depiction, I use k = 1 i.e. in round-1 of cholesky factorization, I compute N - (k + 1) = 2 cells on pivot row i.e. U_{1, i} where i = {2, 3}, while accessing cells from marked submatrix. You may want to take a look at what exactly is computed by each of N - (k+1) work-items here.

After completion of both steps, in each round, all cells of pivot row U_{k, _} hold final value i.e. what it's supposed to be in upper triangular portion after factorization. And after N-many rounds, upper triangular portion is stored in U_{N x N}.

I decide to run benchmarks on updated cholesky factorization implementation. Previous implementation on same hardware performed worse for N = 1024, completing in ~400ms, which is now improved to ~370ms. You may also notice, as matrix dimension keeps increasing, floating point math error also keeps increasing, which is found when comparing L_{N x N} x U_{N x N} with A_{N x N}. As I compile DPCPP program with -ffast-math option, allowing fast, aggressive, lossy floating point computation, I expect deviation of this scale.

Finally I run improved implementation on another CPU, getting to much better performance of ~172ms of completion time, for N = 1024. Previous unoptimised version on same hardware with same launch configurations resulted into completion time of ~221ms --- ~22% performance boost !

I keep optimised implementation of cholesky factorization here for future reference. In coming days, I'll take up other problems for solving them on accelerated environments, as I generally do.

Have a great time !