This week I was trying to implement Matrix Multiplication, on GPGPU using Vulkan Compute API, which is pretty easy to parallelize, given that each cell of resulting matrix can be computed independent of any other cell. This is a simple data parallel problem, where same kernel can be run for each cell of resulting matrix without any data dependency, while input is read from two immutible buffers ( read Matrix A, B ). For understanding performance gain when run on GPGPU, I planned to implement naive matrix multiplication algorithm, which runs with time complexity O(N ** 2), in both CPU & GPU executable form. Given that GPUs are massively parallel machines, multiple cells of resulting matrix can be computed at a time, while paying very low synchronization cost, given nature of problem at hand.
When computing matrix multiplication on CPU, I make use of two nested loops, where each iteration of inner most loop computes value at a certain cell of resulting matrix with formula
C [i, j] = sum([A[i, k] * B[k, j] for k in 0..N]) // N = 4 👇
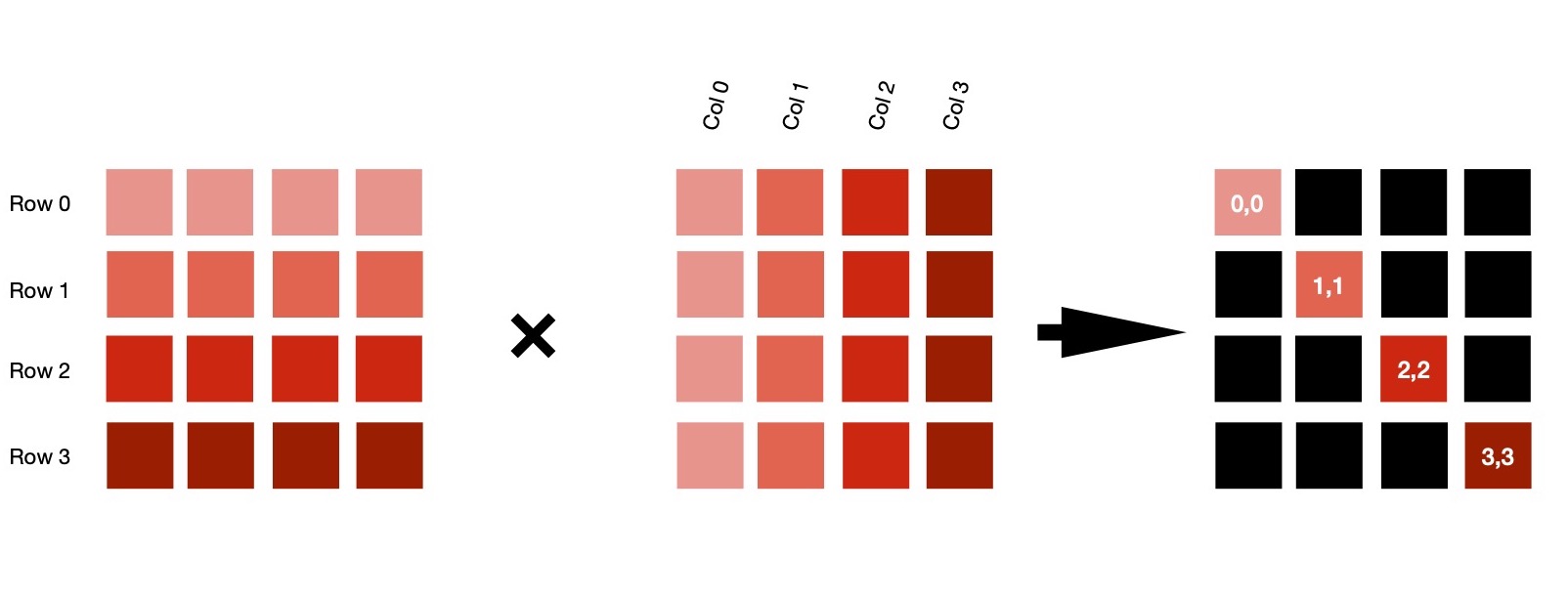
If I work with two 4 x 4 matrices, multiplication algorithm looks like 👇. For making it more generic, first LHS matrix's #-of columns & RHS matrix's #-of rows need to be equal. Otherwise, multiplication is not possible. Two nested loops iterate in such a way so that it's possible to generate indices of each cell of resulting matrix of dimension M x P, when LHS(M x N) & RHS(N x P).
for i in 0..(M = 4) {
for j in 0..(P = 4) {
C [i, j] = sum([A[i, k] * B[k, j] for k in 0..(N = 4)])
}
}
It's clearly understandable that each cell of resulting matrix C can be computed independently --- easily parallelizable. Now each invocation of compute shader ( read kernel running on GPU ) computes single cell of resulting matrix & exits; as many of these invocations can be run by GPU at same time, speed up is quite noticeable.
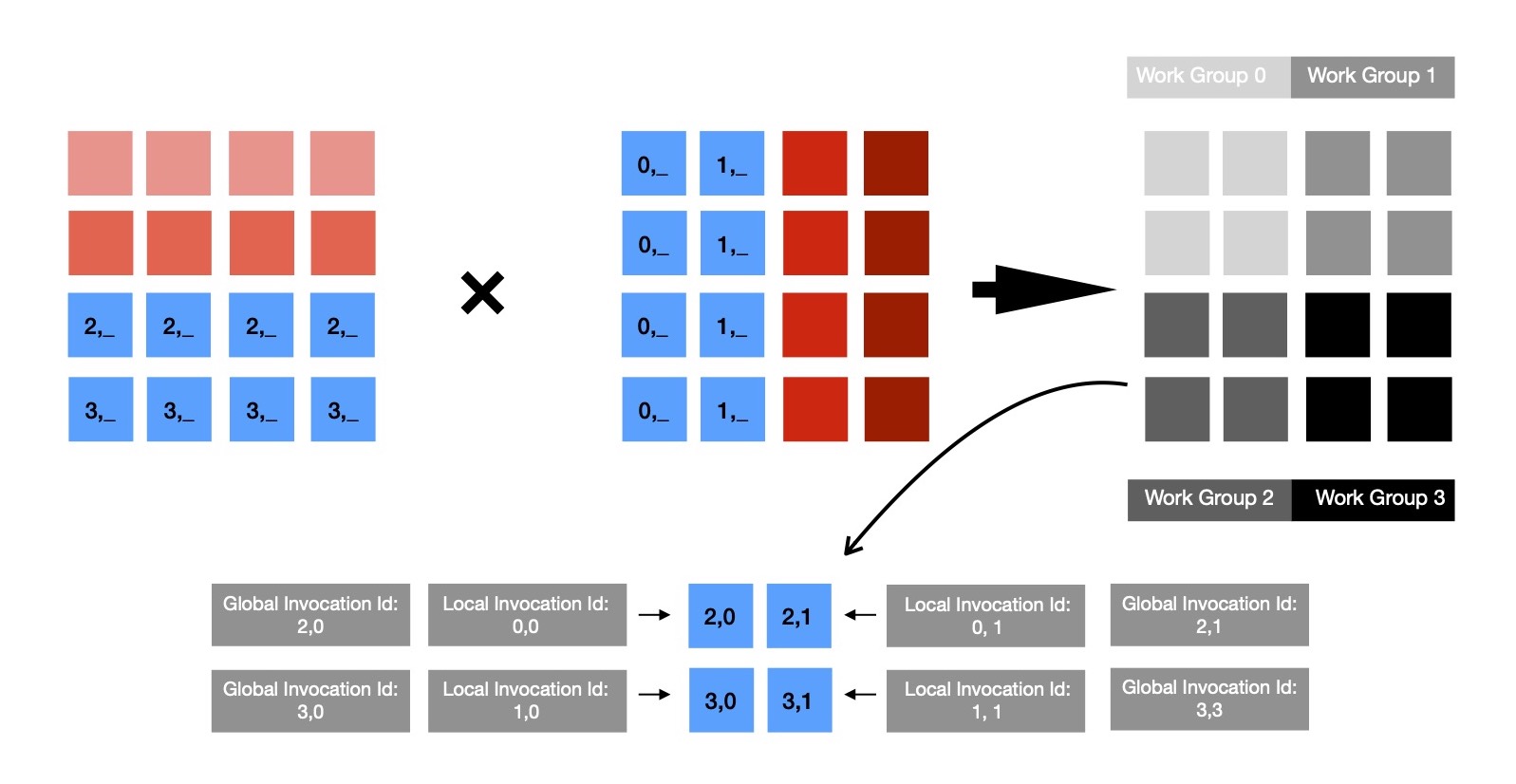
During each invocation of compute shader, following code snippet is run, which reads input from LHS's rowi & RHS's columnj; computes result & finally writes computed value for cell (i, j) at respective memory location. Notice, how one dimensional array being used for respresenting/ accessing two dimensional matrix.
// figure out which cell of resulting matrix is to be computed
// in this invocation
const uint row = gl_GlobalInvocationID.x;
const uint col = gl_GlobalInvocationID.y;
// better to check, so that memory bounds are well respected !
if(row >= 4 || col >= 4) {
return;
}
// compute value at cell (row, col) of resulting matrix
int sum = 0;
for(uint i = 0; i < 4; i++) {
// LHS => matrix_a ( 4 x 4 )
// RHS => matrix_b ( 4 x 4)
sum += matrix_a[row * 4 + i] * matrix_b[i * 4 + col];
}
// store at proper memory address
matrix_c[row * 4 + col] = sum;
Finally, it's time to run both CPU, GPU executable matrix multiplication implementation. Speed up obtained is noticeably large
due to nature of problem & SIMT execution model of GPUs. As I've used an old integrated graphics card, I believe executing same implementation
on discrete compute enabled graphics unit with subgroup size > 32, should result in much better performance. In my case, ~32 invocations execute
in parallel, if subgroup size > 32, no doubt speed up will be visibly higher.
I keep whole implementation here for future reference.
$ cargo run --release
Device: Intel(R) HD Graphics 5500 (BDW GT2)
Vulkan API: 1.2.0
Queue Count: 1 Compute: true Graphics: true
Subgroup Size: 32
GPU matrix multiply: 394.787463ms
CPU matrix multiply: 7.828816465s
Speed Up: 19
In coming days, I'll keep exploring Vulkan Compute more deeply, while implementing GPU executable parallel algorithms.