Speeding up Matrix Multiplication on GPGPU, using SYCL DPC++

Created : September 25, 2021

A few weeks ago I wrote one post, demonstrating parallel matrix multiplication on GPGPU using Vulkan Compute API, where the speed up obtained compared to single threaded version was quite substantial. But last week while working on some other problem, where matrix multiplication was a necessary step, I discovered there are other ways to partition matrix multiplication problem into subproblems, which brings better speed up. These ways leverage GPGPU hardware capabilities in a better fashion, which essentially speeds up this data parallel computation. Matrix multiplication itself is easily parallelizable due to absence of dependencies among computational steps, which requires lesser synchronization, meaning all employed threads can work on a single ( unique ) memory location, without resulting into conflict ( read data races ).

Today I'd like to spend sometime in explaining what I've discovered.

In all version of matrix multiplication each cell of resulting matrix is computed independently, by element-wise multiplying & summing respective row & col. If C[i, j] is being computed then respective thread will read elements from A_{i, _} & B_{_, j} i.e. i-th row of A & j-th column of B and multiply them element-wise, sum of those will be stored in C[i, j]. For square matrices of dimension N x N, it'll result into 2*N-many reads from different memory locations. Each worker thread does same i.e. N*N-many worker threads each to read 2*N values. Operand matrices are stored in global memory, accessing those introduces high latency, resulting into slowed down computation. This issue can be resolved to some extent by making use of local memory available to each work group.

This is how a naive matrix multiplication kernel can be written.

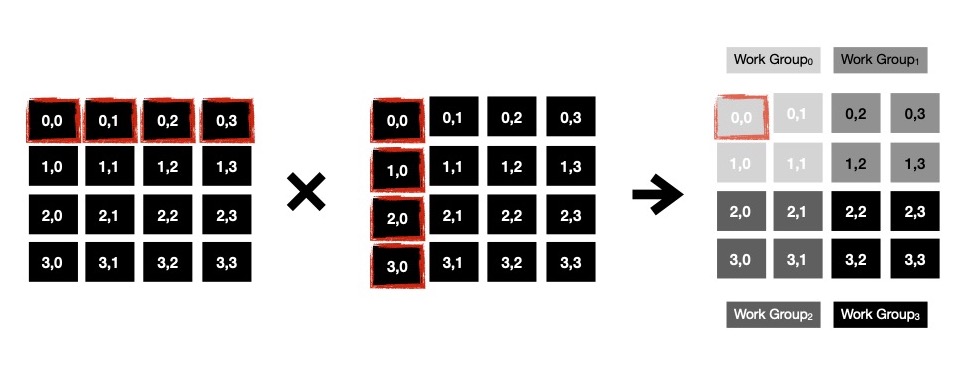
Notice, when WorkGroup₀ computes cells (0, 0) & (0, 1), it accesses same row i.e. A₀ multiple times. Similarly when cell (1, 0) & (1, 1) are computed, row A₁ is accessed multiple times, from global memory. I can club some memory access of cells living in same row of resulting matrix C. I make use of local memory where I store common portion of left operand matrix A i.e. A₀ while computing cell (0, 0) & (0, 1). 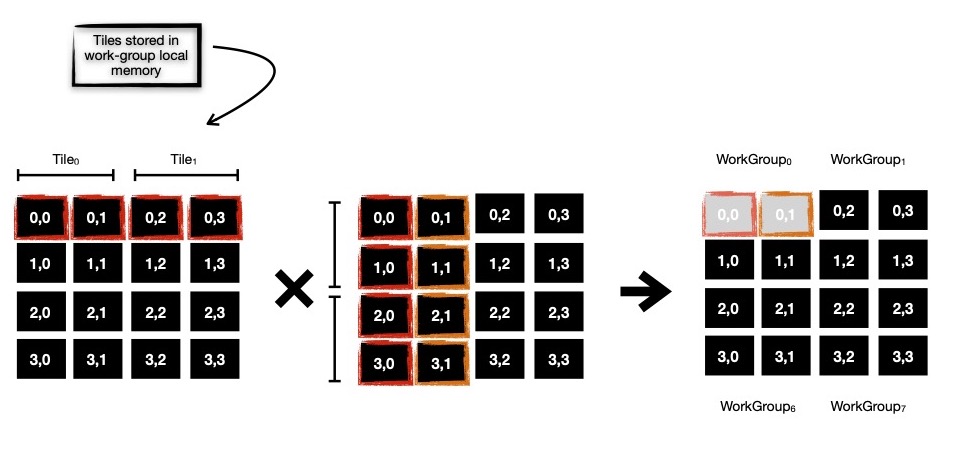In this tiled matrix multiplication, each work group uses 1-dimensional local buffer to store tile ( read portion of cells from left multiplicand matrix ). When computing cells, some operands are read from local memory ( think of it as cache, living in faster memory ), which is faster than global memory, resulting into speed up. But also notice, if I'm going to make use of local memory, I should first make sure this local memory is filled up, before it's used as operand store. This calls for making use of barriers, which provides me with nice synchronization technique among all work items of work group in execution. Using barrier, ensures all work items are going to see all side effects, performed by other work items in same work group, once past the barrier. Along with memory visibility guarantee, it also gives one execution flow guarantee, where it's ensured that until all work items of same work group arrive at that barrier, none will be able to proceed. After this barrier, each work item can proceed with tiled cell computation. Only I need to make sure tile width properly divides width of matrix i.e. N.

I notice one more thing, if I consider using 1D local buffer along with 2D workgroup size, it'll result into data race. If I keep using 2D workgroup size, WorkGroup₀ computes cell (0, 0), (0, 1), (1, 0) & (1, 1). Now cell (0, 0) & (0, 1) are interested in same row of operand matrix A, while cell (1, 0) & (1, 1) are interested in something else. With 1D local buffer, work items computing cell (0, 0) & (0, 1) attempts to fill up buffer with elements of A₀, whereas work items (1, 0) & (1, 1) attempt to do same on same memory slice --- data race.

For avoiding this problem, I simply use 1D local buffer of width B along with workgroup size of (1, B), so that only cells across same row are computed by work items in same workgroup --- no more data race.

I found, introduction of local memory buffer in matrix multiplication kernel speeds up computation but it calls for more synchronization among work-items in a work-group, using barrier(s). Synchronization burdens work items, lowering speedup which could be obtained in absence of them.

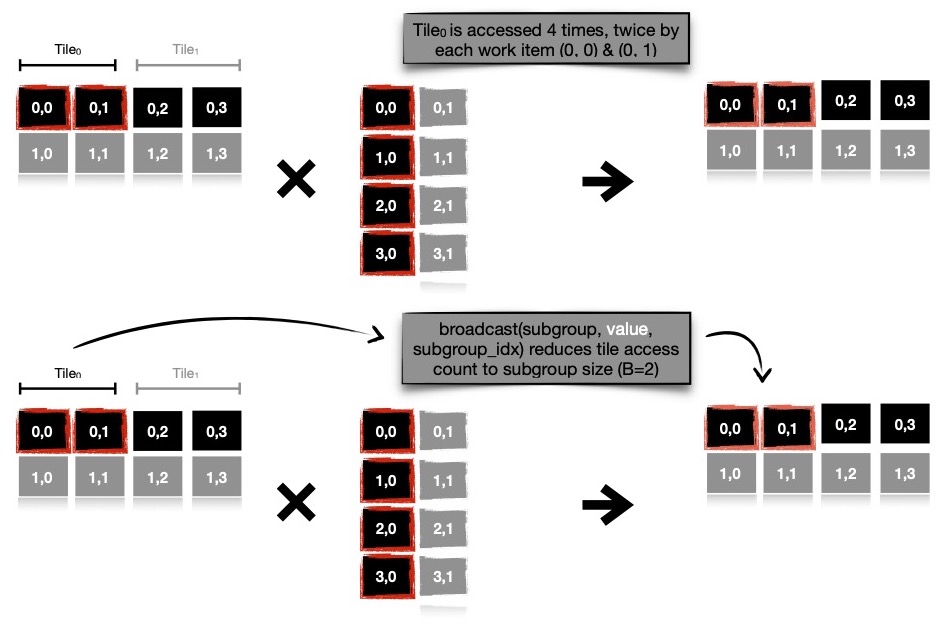
So I discovered subgroups, which can be considered subset of work-items in a work-group. Subgroups provide me with powerful in-built functions, which can be applied on whole work group itself, rather than each work item applying on self & then synchronizing using other means like barrier. Notice, I'm using 1D local buffer of width B, where B work items accessing B memory locations from local buffer --- resulting into total B*B memory accesses for each tile. Let's take a look at this code snippet from last kernel.

As I mentioned subgroup collective functions can be applied on whole subgroup, instead of each individual work items, this can be leveraged for reducing B*B memory accesses for each tile to only B many of those. Single work item reads memory address acc_local[i], remaining (B-1)-many work items hear broadcast. Broadcast collective function gives me way to avoid barriers --- substantiallly decreasing explicit synchronization cost. This approach indeed enhances computational speed up obtained.

I run 3 parallel matrix multiplication implementations with 1024x1024 operand matrices, in order, on both CPU & GPGPU and obtain following result. It's clearly understandable that subgroup collective function based implementation produces impressive result on GPGPU, due to in-built hardware support for low-cost synchronized computation/ communication. When running on CPU, I use workgroup size of B = 4, on the other hand when running on GPU, I use workgroup size of B = 32. These are preferred subgroup sizes of respective implementations.

I keep all these implementations here for future reference. In coming days, I plan to explore heterogeneous parallel programming with SYCL DPC++ more, while implementing other algorithms & sharing my understanding.

Have a great time !